高数一公式
极限与连续
极限
运算法则
若
和差的极限等于极限的和差
乘积的极限等于极限的乘积
商的极限等于极限的商
当时, 常数的极限等于常数
求极限
代入法
分母不为零时可用代入法求极限
约去为零公因子法
找出并约掉分子分母中为零的公因子
分子分母同时除最高次项
等价代换法
当
常数中只有 0 可以看作无穷小
当
时 的绝对值无限增大 则称 为 时的无穷大量 无穷小量(不为 0时)和无穷大量互为倒数
设 α,β 都是自变量 x 在同一变化时的无穷小量,且极限
- 若
,称 α 是比 β 高阶的无穷小 - 若
,称 α 是比 β 低阶的无穷小 - 若
,称 α 是比 β 同阶无穷小;当 c = 1 时,称 α 是比 β 等价无穷小记为
常用等价无穷小代换并非所有的无穷小都可以比较 如
时 x 和 都是无穷小,就不可比较 等价代换法只能用于乘除不能用于加减
两个重要极限
或 或
连续性
- 有定义
- 左右极限存在
- 左右极限等于该点函数值
导数
基本公式
求导
常见求导公式
- *
- *
- *
ln常数的导数为0 - *
- *
- *
- *
- *
- *
特殊的公式
- *
常数可以提取出来
* 标记的重点记
运算法则
- 和差的导数等于导数的和差
- 积的导数等于前导后不导加上前不导后导
- 商的导数等于上导下不导减上不导下导除以下的平方
复合函数求导
定义
但是
求导
- 假设
- 分别求导
- 回代
eg:
微分方程
其他资料
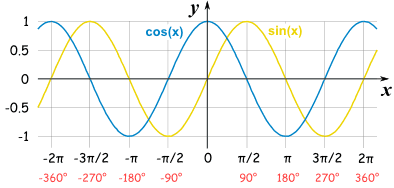
- 正弦/余弦函数图象:
- 十字相乘法