day1高数一极限
准备
略
考情分析(00:02:32 - 00:33:42)
略
极限与连续(00:33:42 - end)
本节内容 天一成考 高等数学(一) p1 - p5
定义(00:33:42 - 00:39:49)
略
运算法则(00:39:49 - 00:42:33)
若
和差的极限等于极限的和差
乘积的极限等于极限的乘积
商的极限等于极限的商
当时,
常数的极限等于常数
求极限(00:42:33 - end)
代入法(00:42:33 - 01:17:06)
分母不为零时可用代入法求极限
练习
解:
根据正弦/余弦函数图象:
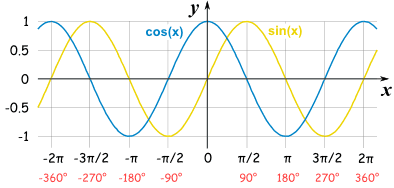
可得
解:
解:
解:
解:
解:
真题
解:
根据正弦/余弦函数图象:

可得
解:
根据正弦/余弦函数图象:

可得
解:
解:
解:
- 休息(01:03:52 - 01:12:43)
解:
解:
约去为零公因子法(01:17:06 - 01:33:10)
找出并约掉分子分母中为零的公因子
练习
解:
分子使用十字相乘法得出
解:
解:
分子分母同时除最高次项 (01:33:10 - 01:36:53)
练习
解:
等价代换法
定义
当
常数中只有 0 可以看作无穷小
当时 的绝对值无限增大 则称 为 时的无穷大量
无穷小量(不为 0时)和无穷大量互为倒数
无穷小量的比较
设 α,β 都是自变量 x 在同一变化时的无穷小量,且极限
- 若
,称 α 是比 β 高阶的无穷小 - 若
,称 α 是比 β 低阶的无穷小 - 若
,称 α 是比 β 同阶无穷小;当 c = 1 时,称 α 是比 β 等价无穷小记为
常用等价无穷小代换并非所有的无穷小都可以比较 如
时 x 和 都是无穷小,就不可比较
等价代换法只能用于乘除不能用于加减
练习
解:
解:
解:
解:
根据正弦/余弦函数图象:
可得
本节练习
其他资料
- 正弦/余弦函数图象:

- 十字相乘法